Laboratorio de Automatización y Control de Sistemas Dinámicos
Para esta semana hay que investigar acerca de unos temas que nos dieron la semana pasada.
A mi me toco acerca de la función Escalón, Rampa e Impulso; a continuación hablare de ellos:
Función Impulso:
La función del impulso usualmente se escribe comoδ(t)
La manera para ver como es la gráfica es usar un pulso rectangular que va dea−ε2 a a+ε2 con una altura de 1ε .
Al momento de tomar su límite,limit ε→0 , podemos observar que su ancho tiende a ser cero y su altura tiende a infinito (Llegando a parecerse a una línea recta como la imagen al principio) conforme su área total permanece constante con un valor de uno.
La forma del movimiento de la función se muestra abajo.

Función Impulso:
La función del impulso usualmente se escribe como
La manera para ver como es la gráfica es usar un pulso rectangular que va de
Al momento de tomar su límite,
La forma del movimiento de la función se muestra abajo.
Vídeo acerca de la explicación de esta función:
Referencias:
http://es.wikipedia.org/wiki/Delta_de_Dirac
http://en.wikipedia.org/wiki/Dirac_delta_function
http://cnx.org/content/m12824/latest
http://mathworld.wolfram.com/DeltaFunction.html
http://www.wikimatematica.org/index.php?title=Funci%C3%B3n_Delta_de_Dirac
Referencias:
http://es.wikipedia.org/wiki/Delta_de_Dirac
http://en.wikipedia.org/wiki/Dirac_delta_function
http://cnx.org/content/m12824/latest
http://mathworld.wolfram.com/DeltaFunction.html
http://www.wikimatematica.org/index.php?title=Funci%C3%B3n_Delta_de_Dirac
Función Escalón:
Conocida como Función Escalón de Heaviside, también conocida como Función Escalón Unitario.
Esta función se utiliza en ingeniería de control y procesamiento de señales, representando una señal que se enciende en un tiempo específico, y se queda encendida indefinidamente.
O sea el representar el caso de un interruptor que permanece abierto hasta que en un instante se apaga, estableciendo el máximo voltaje a una carga.
Esta función se utiliza en ingeniería de control y procesamiento de señales, representando una señal que se enciende en un tiempo específico, y se queda encendida indefinidamente.
O sea el representar el caso de un interruptor que permanece abierto hasta que en un instante se apaga, estableciendo el máximo voltaje a una carga.
El valor de salida de esta función es 1 cuando los argumentos (el valor de la variable) de la función son Positivos y es 0 cuando los argumentos son negativos.
H(x) = Nombre con el que se conoce a la Función Escalón
u(x) = Función a evaluar
Si el valor de X es menor a 0 o negativo el valor de salida es 0; si el valor de X es mayor a 0, el valor de salida es 1.
La unica duda con lo anterior es si x = 0, este dato no esta bien definido ya que algunos le dan el valor de 1 y otros le dan el valor de 1/2 para que le de un parecido a la grafica que puse al principio.
A continuación pongo los valores de salida que tendria la Escalón si se respetara lo anterior.
Ejemplo de la Función Escalón:
Se tiene una función (Cualquiera que desees) y después se tiene una tabla con valores de X (Como para resolver las ecuaciones; teníamos los valores de x y sacábamos lo de y, estos valores de x se compararían con lo anterior, así que todo los valores de x que sean mayores a 0 el valor de y sería 1 y así hasta encontrar todos los valores de la tabla. )
Una vez hecho lo anterior solo seria el Graficar los valores de X y de Y y la gráfica daría la estructura de la función Escalón.
Ya por ultimo
Se tiene una función (Cualquiera que desees) y después se tiene una tabla con valores de X (Como para resolver las ecuaciones; teníamos los valores de x y sacábamos lo de y, estos valores de x se compararían con lo anterior, así que todo los valores de x que sean mayores a 0 el valor de y sería 1 y así hasta encontrar todos los valores de la tabla. )
Una vez hecho lo anterior solo seria el Graficar los valores de X y de Y y la gráfica daría la estructura de la función Escalón.
Ya por ultimo
En términos sencillos esta Función es la integral definida desde -Infinito hasta el valor de la variable (x) de la Función Impulso.
Para terminar este punto anexo un video donde explican esta función:
Referencias
http://es.wikipedia.org/wiki/Funci%C3%B3n_unitaria_de_Heaviside
http://ejerciciosdefunciones.com/ejemplo-de-funcion-escalon/
http://mathworld.wolfram.com/HeavisideStepFunction.html
http://www.wikimatematica.org/index.php?title=Funci%C3%B3n_Heaviside
Función Rampa
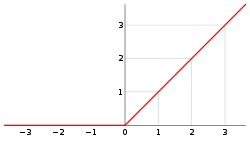
Se la da el nombre de "función rampa" gracias a la forma de su gráfica.
w
La Función 'r(t)' se define como 'El valor de r(t) es igual a t si t es mayor o igual a 0 y r(t) es igual a 0 si t es menor que 0':
La derivada de esta función es igual a la de la Función Escalón.
Referencias
http://es.wikipedia.org/wiki/Funci%C3%B3n_rampa
http://ingeniedia.blogspot.mx/2010/10/funcion-rampa.html
http://www.scribd.com/doc/22359951/GRAFICO-DE-UNA-FUNCION-UTILIZANDO-SENALES-ELEMENTALES
En General
http://es.wikipedia.org/wiki/Funci%C3%B3n_unitaria_de_Heaviside
http://ejerciciosdefunciones.com/ejemplo-de-funcion-escalon/
http://mathworld.wolfram.com/HeavisideStepFunction.html
http://www.wikimatematica.org/index.php?title=Funci%C3%B3n_Heaviside
Función Rampa
Se la da el nombre de "función rampa" gracias a la forma de su gráfica.
w
La Función 'r(t)' se define como 'El valor de r(t) es igual a t si t es mayor o igual a 0 y r(t) es igual a 0 si t es menor que 0':
La derivada de esta función es igual a la de la Función Escalón.
Referencias
http://es.wikipedia.org/wiki/Funci%C3%B3n_rampa
http://ingeniedia.blogspot.mx/2010/10/funcion-rampa.html
http://www.scribd.com/doc/22359951/GRAFICO-DE-UNA-FUNCION-UTILIZANDO-SENALES-ELEMENTALES
En General
En base a todo lo anterior tenemos que la Función Escalón es la Integral de la de Impulso y la de Rampa es la Integral de la de Escalón, por lo tanto estas Funciones y en pocas palabras cada función depende de otra, la única que no depende de ninguna es la de Impulso.



Está bien. Se me hace raro tu uso de mayúsculas iniciales. Van 15 pts.
ResponderEliminar