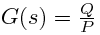Entrada Final

Liga en donde esta la entrada:

http://autoycontrolave.blogspot.mx/2012/11/proyecto-automatizacion-y-control.html

Entrada # 6

Laboratorio de Automatización y Control de Sistemas Dinámicos

Para esta semana me toco realizar el siguiente problema:

Viendo este problema tenemos que consiguir la señal de control óptima esta comúnmente se determina con:

Ya con esto el siguiente paso sera el analizar la ecuación J.

Teniendo:

Sustituimos el valor de U:

Teniendo lo siguiente:

Para cumplir con lo anterior hacemos el valor de Q por I, por lo tanto la factorización queda:

Teniendo la ecuación:

Sustituimos R por I, nos queda:

De la siguiente ecuación, el valor de R⁻¹ se elimina, quedando:

Teniendo la ecuación de matrices de Riccati:

Teniendo que la transpuesta de B:  

Y P:

Tenemos:

Por lo tanto ya que los valores de K son 1 se sustituyen en lo que vale U, lo que nos deja por ultimo:

Referencias:

Modern Control Engineering Fourth Edition
Katsuhiko Ogata

Reporte Propiedades Estructurales

Esta actividad la hice solo ya que mi compañero me dejo solo.

Pdf del Reporte en LaTex.
https://www.dropbox.com/s/7kt9y94e86kh0p7/entrada.pdf

Código del Pdf



Código de las imágenes.

Puntos Extra

Resumen del Artículo

Coverage Control for Mobile Sensing Networks

(Control de cobertura para las redes de detección móviles)

Este artículo nos habla acerca de algoritmos para el control y la coordinación de los vehículos autónomos (aquellos que tienen la capacidad de manejarse por su propia cuenta).

Estos vehículos son utilizados como sensores móviles (estos se sintonizan dependiendo la búsqueda), para poder realizar detecciones mediante estos.

Cabe aclarar que los algoritmos no son los encargados de la detección (esto lo hacen los sensores); estos se encargan de definir la forma correcta con la que la cobertura sea lo mas óptima y de definir las políticas mediante la cual se realizara la detección.

Todos los algoritmos presentados en el articulo son basados en el problema del Descenso mas Pronunciado (Gradiente), este nos dice que se encarga de buscar un mínimo que este asociado a la resolución de secuencial de varios problemas.

La estructura común de estos algoritmos es el siguiente:

Tipos de Control 
Hace uso de los sistemas distribuidos para hacer uso de los sensores con los que cuenta cada automóvil.

Referencias:

http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1284411

http://www.investigaciondeoperaciones.net/metodo_del_gradiente.html

Entrada # 5

Laboratorio de Automatización y Control de Sistemas Dinámicos

Para esta semana consistió en elegir un problema y resolverlo, el elegido es el siguiente:

Considere el sistema en lazo cerrado con la siguiente función de transferencia en lazo abierto: Dibuje los diagramas polares directo e inverso de G(s)H(s) con K = 1 y K = 10.

Aplique el criterio de estabilidad de Nyquist a las gráficas y determine la estabilidad del sistema con estos valores de K.

Primeramente que son los siguientes conceptos:

Diagrama Polar

Representación de la función de transferencia senoidal, G( jω) , en coordenadas polares, para
variaciones de ω  entre 0 e ∞

Son conocidos también como Diagrama de Nyquist.

Criterio de Nyquist

Medio encargado en estudiar la estabilidad en el dominio de la frecuencia.

Relaciona la respuesta en frecuencia de lazo abierto con el número de polos y ceros de la ecuación característica ubicados en el SPD.

Referente al problema hay que considerar unos puntos:

Para obtener el resultado de Nyquist, existe una función en Octave, mediante el paquete signal, que se llama nyquist().

Aquí incluyo el código en Octave:


Imagenes del resultado:

con K = 1

con K = 10

Observando las gráficas vemos que las dos están de 0 a -infinito por lo tanto las dos gráficas son estables.

Referencias:

http://www.disa.bi.ehu.es/spanish/profesores-etsi-bilbo/~jtpirgoe/Tema_7_Diagrama_Nyquist%20.pdf

Entrada # 3

Programa # 1 Estabilidad

Para esta ocasión tenemos que demostrar la estabilidad de nuestras funciones de transferencia, antes de comenzar les muestro nuestra función:

A continuación tenemos el comportamiento de los polos y ceros en forma gráfica de la función de transferencia:

Como vemos en la imagen vemos en la imagen, la función tiende a ser estable hasta un cierto punto en el cuál su comportamiento se vuelve inestable.

Después tenemos el código utilizado como vemos en los comentarios, los valores de la Resistencia y el Calor son Constantes, estos son inicializados a 1 para que no apliquen un gran cambio en el resultado:

El resultado del código lo mostramos a continuación, el resultado no muestra el comportamiento con distintas Intensidades de entrada y con sus respectiva gráfica cuando se le aplica un ruido (este ruido fue realizado mediante la función seno y un tiempo de 0 y 20 con .001 entre cada uno):

Con 2

                                                                        Entradas

                                                                       Con Ruido

Con 12

                                                                                Entradas

                                                                               Con Ruido

Con 32

                                                                               Entradas

                                                                             Con Ruido

Con 100

                                                                                Entradas

                                                                               Con Ruido

Como vemos en todas las imágenes anteriores, las gráficas nunca se detienen en un punto en especifico, por lo tanto se mantiene la propuesta de que nuestra función tiende a ser inestable.

Entrada # 4

Laboratorio de Automatización y Control de Sistemas Dinámicos

Para esta semana consistió en elegir un problema y resolverlo.

Primeramente el Problema Elegido:

Determine el rango de valores de K para la estabilidad de un sistema de control con realimentación unitaria cuya función de transferencia en lazo abierto es

En base al libro de Ogata nos dice que para los problemas de estabilidad hay que multiplicar el denominador y nominador con tal de que no exista multiplicación alguna en ellos, quedaría:

Pero como tenemos un valor en el numerador tenemos que pasarlo al denominador, nos quedaría:

Tenemos que:

Y

En base a las ecuaciones anteriores nos quedaría lo siguiente:

En base a la imagen anterior nos quedaría que:

Para determinar el rango de K habrá que tomar los términos de s que contengan a K e igualarlos a 0 cada uno, y esos dos valores serian el rango de K.

------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------

Por lo tanto el rango de K debería de ser:

y

 O dicho de otra manera:

Referencias:

Modern Control Engineering Fourth Edition
Katsuhiko Ogata

Entrada 2

Automatización y Control de Sistemas Dinámicos

Diagrama de Bloques

Para esta entrada consiste en mostrar el diagrama de bloques de la función de transferencia de nuestro proyecto.

Antes de hacer esto, completare la función de transferencia que había hecho en el reporte pasado.

Viendo los valores de entrada y salida (http://materiasdepedrito.blogspot.mx/2012/09/reporte-1.html) tenemos que:

El valor de entrada sería seria la Potencia de la corriente eléctrica, la ecuación de esta es:

P = Potencia de la corriente eléctrica.

I = Intensidad de la corriente.

R = Resistencia del material del que esta hecho la punta del cautín.

dq/dt = Derivada del calor respecto al tiempo.

El valor de salida seria el Calor producido por el cautín, la ecuación de esta seria:

Q = Calor

m = Masa del Cautín

c = Calor especifico del cautín

Delta T = Diferencia de Temperaturas (Entrada y de Salida)

Teniendo esto la función de transferencia seria:

Aplicando la transformada de Laplace a cada una de las funciones:

Función de Entrada

Función de Salida

Aplicando la estas funciones a la de transferencia tenemos nuestra función de transferencia

Ya a continuación muestro el diagrama de bloques: