Materias 7mo Semestre

jueves, 18 de octubre de 2012

Entrada # 7

Reporte # 2

Blocks Ciphers

First shall begin with a little explanation about what this is.

Consists of a symmetric key cipher (in which the same key is used to encrypt and decrypt messages) that operates on groups of bits of fixed length, called blocks, applying a transformation invariant.

When performing encryption, this takes a block of plain text as input and produces a ciphertext of the same size as the original text.

For this week is to choose one of the existing encrypted and explain.

Akelarre Cipher

Who and When Proposing

Was design for G. Álvarez Marañón, D. Guía Martínez, F. Montoya Vitini, A. Peinado Domínguez in 1996.

Mejoras que tenía de los ya existentes

Akelarre combines the best of this cipher's:

IDEA.- Handles multiple arithmetic.
RC5.- Rotation of Keys.

This encryption aims to be a strong encryption system most efficient.

How it Works

First we have a define the next points:

Variable numbers of rounds

The autors claim the 4 rounds is more safe.
Although the reality is unsafe for any number of rounds!

Block length is 128 bits

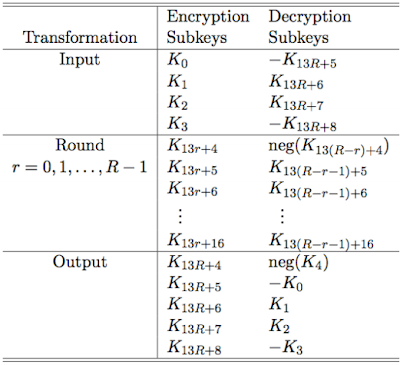
Key length can be any multiple of 64 bits

The common lenght of the key is the 128 bits.

Lots of blocks subkey: 13R + 8

Every of the subkeys its a word of 32 bits.

Mod also employs 232 and XOR

Adding rotation (AR) structure

Proceso del Cifrado

For the encryption:

Inputs data, this we have transformating for your use
Round 0,1,2, ..., R-1
Cifred data

Explain of more extensing form:

Taking:

(A0, A1, A2, A3), this would be the input to round r.
(B0, B1, B2, B3), the output would rotation keys.

Then Apply the struct of Akelarre
(B0, B1, B2, B3) = (A0, A1, A2, A3) <<<<

Where "<<<" is left rotation and $(X)_i_\ldots_j$ , this means bits i thru j (inclusive) of X

Recall, the bits enumerating the left to right, started in 0

Explain of visual form:

Where:

W = X
W1 make first
Rotate 31 bits, with 1 bit fixed

Taking:

(T0 ,T1), output would AR structure

(T0 ,T1) = AR(B0 ⊕ B2, B1 ⊕ B3), indicating the input values and which has the form AR obtain these.

Later:

(D0, D1, D2, D3), output would round r.

Then:

(D0, D1, D2, D3) = (B0⊕T1, B1⊕T0, B2⊕T1, B3⊕T0)

One Time to Finished This:

The Block (D0, D1, D2, D3) whold:

The entrance of the next round.
If the last one, whold the output of all the process.

For the decryption process would use the same process only data that would introduce a little different.

Math Type which is based

As based on IDEA uses XOR (⊕) combined with rotation values, and modular arithmetic.

Example

The following is a problem which show difficulties if used have certain values in this.

-------------------------------------------------------------------------------------------------------------------

Only to start:

z is K in the explication.

Given X = (0x53,0x8d,0x86,0x80), Y = (0x74,0x21,0x9c,0xca):

Create an equation, substituting in the values for x and y:

(0x53-z5) ^ 0x86 ^ z7 = (0x74 + z1) ^ 0x9c ^ z3

Starting with the low-order bit (denoted zi[0]), determine which of the following bit combinations solve the above equation:

(z5[i],z1[i],z3[i]^z7[i]) = ((0,0,0),(0,0,1),...,(1,1,0),(1,1,1))

Provided sufficient plaintext-ciphertext pairs, it should theoretically be possible to uniquely determine the values of the unknown subkeys using this technique.

In order to solve for the unknown plaintext, we need to solve the below equation:

We know the entire right-hand side of the equation and z1 on the left-hand side.

Given sufficient redundancy, it is possible to determine the values of x1 and x3. The papers we read did not go into detail about how to perform this recovery.

Determining z1...z8:

Tried multiple approaches that either resulted in hundreds of potential subkey values, or did not find a single subkey value

Bit-by-bit as described

Resulted in hundreds of matches

Bit-by-bit, taking carry bits into consideration

Resulted in zero matches

Byte-by-byte bruteforce attack

Worked if the input size was a single byte, but did not work otherwise

-------------------------------------------------------------------------------------------------------------------

Let

A = (A0, A1, A2, A3), be input to round r
U = (U0, U1, U2, U3), be result of rotation
T = (T0, T1), be output of AR structure
B = (B0, B1, B2, B3), be output of round r

Denote A = (a0 ,a1,…,a127)

And similarly for U,T,B

Let l be size of keyed rotation

Then U = (A <<< l) and (B0, B1, B2, B3) = (U0⊕T1, U1⊕T0, U2⊕T1, U3⊕T0)

It follows that B0⊕B2 = U0⊕U2 and B1⊕B3 = U1⊕U3

AR structure has vanished!

The crucial observation for attack

Atacks Y/O Vulnerabilities

Akelarre shows that your design is complicated encryption.

An attack is conceptually simple, but the details are not so simple.

There is an attack in the year 1997, using Ciphertext-only attack.

It therefore proves to be very vulnerable to attacks.

References:

http://www.schneier.com/paper-akelarre.pdf
http://es.wikipedia.org/wiki/Akelarre_(cifrado)
http://www.sacconference.org/proc/SAC_96_002.pdf
http://es.wikipedia.org/wiki/Cifrado_por_bloques
http://en.wikipedia.org/wiki/Akelarre_(cipher)
http://cs.sjsu.edu/~stamp/crypto/PowerPoint_PDF/12_Akelarre.pdf

martes, 9 de octubre de 2012

Entrada 2

Automatización y Control de Sistemas Dinámicos

Diagrama de Bloques

Para esta entrada consiste en mostrar el diagrama de bloques de la función de transferencia de nuestro proyecto.

Antes de hacer esto, completare la función de transferencia que había hecho en el reporte pasado.

Viendo los valores de entrada y salida (http://materiasdepedrito.blogspot.mx/2012/09/reporte-1.html) tenemos que:

El valor de entrada sería seria la Potencia de la corriente eléctrica, la ecuación de esta es:

$P = \frac{dq}{dt} I R$

P = Potencia de la corriente eléctrica.

I = Intensidad de la corriente.

R = Resistencia del material del que esta hecho la punta del cautín.

dq/dt = Derivada del calor respecto al tiempo.

El valor de salida seria el Calor producido por el cautín, la ecuación de esta seria:

Q = Calor

m = Masa del Cautín

c = Calor especifico del cautín

Delta T = Diferencia de Temperaturas (Entrada y de Salida)

Teniendo esto la función de transferencia seria:

Aplicando la transformada de Laplace a cada una de las funciones:

Función de Entrada

$X(s) = L\left\{{\frac{dq}{dt} I R}\right\}$

Función de Salida

$Y(s) = L\left\{{c m \Delta T}\right\}$

$Y(s) = \frac{c m \Delta T}{s}$

Aplicando la estas funciones a la de transferencia tenemos nuestra función de transferencia

$G(s) = \frac{\frac{c m \Delta T}{s}}{sQ(s) I R }$

$G(s) = \frac{\frac{c m (T_f - T_o)}{s}}{sQ(s) I R }$

Ya a continuación muestro el diagrama de bloques:

jueves, 20 de septiembre de 2012

Entrada # 3

Laboratorio de Automatización y Control de Sistemas Dinámicos

Para esta semana, al igual que la anterior, consistió en elegir un problema y resolverlo.

El problema nos dice:

"Considere el que sistema que se muestra a continuación. Calcular la expresión del error en estado estacionario cuando están presentes tanto la señal de entrada de referencia R(s) como la entrada de perturbación D(s)."

Primeramente definir unos conceptos:

Entrada de Referencia.- Impulsos que se le dan al sistema para observar las salidas que tendrían el sistema.

Entrada de Perturbación.- Señales que tienden a afectar al sistema, afectan la salida del sistema; como esta señal es una entrada, por lo tanto esa es externa y se genera fuera del sistema.

Expresión de Error.- Es un valor que nos indica el rango que nos daria el sistema.

De nuestro problema tenemos los siguientes:

Entrada de Referencia R(s), Entrada de Perturbación D(s) y la Expresión de Error es E(s); C(s) seria la salida que produzca el sistema.

El problema nos pide encontrar la Expresión de Error en estado estacionario (No hay algo externo, aparte de lo mencionado, que pueda afectar la salida) cuando están presentes tanto la señal de entrada de referencia como la entrada de perturbación.

La Expresión de Error se calcula como la suma de salidas (La Esperada + la Producida en estado estacionario), en base a las variables y las definiciones tenemos:

La Esperada seria cuando solamente este presente la variable de referencia en el sistema (para este no incluiremos la de perturbación)

La Producida seria las salidas usando solamente la entrada de perturbación (ya que la referencia se vuelve constante y la de perturbación daría un resultado distinto).

Por lo tanto la ecuación de Error seria:

Y ya que como es estacionario tiene que ver con el tiempo nos queda que:

E(s) = E_e_e (t) = E_e_e_R (t) + E_e_e_D (t)

El siguiente paso seria solucionar cada uno de los errores, aquí comenzaremos por el de referencia.

Antes de encontrar cuando el de referencia sea estacionario primero habrá que determinarlo cuando no este así.

Este error se calcula como el valor de la referencia menos la salida producida por el efecto de este:

Teniendo que la salida de sistema es:

Tenemos que $\frac{C_R(s)}{R(s)} = \frac{G_1(s) G_2(s)}{1 + G_1(s) G_2(s)}$

Sustituyendo el error de la referencia en la ecuación.

$E_R(s) = R(s) - C_R(s) = R(s)[1 -\frac{C_R(s)}{R(s)}]$

$E_R(s) = R(s)[1 - \frac{G_1(s) G_2(s)}{1 + G_1(s) G_2(s)}]$

$E_R (s) = {[\frac{1}{1 + G_1(s) G_2(s)}R(s)]}$

Ya aplicandolo de forma estacionaria la de referencia

$E_e_e_R (t) = \displaystyle\lim_{t \to\infty}E_R(t) = \displaystyle\lim_{s \to\ 0} s E_R(s)$

$E_e_e_R (t) = \displaystyle\lim_{s \to\ 0} {s [\frac{1}{1 + G_1(s) G_2(s)}R(s)]}$

Ahora aplicando a las Perturbaciones

$E_D(s) = 0 - C_D(s) = - C_D(s) = - \frac{C_D(s)}{D(s)} D(s)$

Teniendo que: $\frac{C_D(s)}{D(s)} = \frac{G_2(s)}{1 + G_1(s) G_2(s)}$

$E_D(s) = - \frac{G_2(s)}{1 + G_1(s) G_2(s)} D(s)$

Sacando la forma estacionaria de las perturbaciones

$E_e_e_D (t) = \displaystyle\lim_{t \to\infty} E_D(t) = \displaystyle\lim_{s \to0} s E_D(s)$

$E_e_e_D (t) = \displaystyle\lim_{s \to0} [-\frac{G_2(s)}{1 + G_1(s) G_2(s)} D(s)] s$

Sustituyendo las estacionarias:

$E_e_e (t) = \displaystyle\lim_{s \to\ 0} {s [\frac{1}{1 + G_1(s) G_2(s)}R(s)]} + \displaystyle\lim_{s \to0} [-\frac{G_2(s)}{1 + G_1(s) G_2(s)} D(s)] s$

Referencias

http://www.slideshare.net/ptah_enki/definiciones-de-control-326816
http://isa.uniovi.es/docencia/raeuitig/tema1.pdf

Entrada # 6

Implementing the RSA algorithm in an HTTP (Authenticating Users)

For this week we have to implement the RSA algorithm into a web server.

Be has a user to validate your user name, for it makes use of the RSA algorithm, the server and the client need certain values (the server already has the information about your name and values of 'e' and 'n 'while the client would have' d 'and' n ').

The process would be the client requests a value of 'x' to the server, this does just that along with the link to download a script to determine the values of 'and' and 'r'.

The client downloads this file and determines the values mentioned above, then the client will provide the server user your name (as must be added, only find the name that is to avoid errors Language Script) together with the value of 'r '.

The server receives this data and using the user name extracts the values of 'e' and 'n' (for storing information this data can use files or databases) and together with the value of 'x' that provides the client.

Obtains two different 'y' (one with a specific function for us - this function is the same as in the script that I download the client - and by the formula r ^ e mod n) and compare these values, if these are the same you sends a message to the user indicating that authentication was successful.

Code in PHP
Script of Python Code of SQL

Vídeo mostrando la ejecución
En Proceso

jueves, 13 de septiembre de 2012

Entrada # 5

Implementación de la Autentificación RSA

En este código se hicieron todos los cálculos para encontrar los valores de n, d y e y los guarda en un archivo junto con los nombres de usuario.

Como logran ver los valores de d y de p y q fueron asignados por mí (Obviamente respetando las reglas).

El orden del texto es: Usuario, valor de e, valor de d y valor de n

Imágenes donde se determino el valor de d:

Después se muestra los códigos donde se hizo uso de los sockets

Cliente

Servidor

Referencias:

http://mundogeek.net/archivos/2008/04/12/sockets-en-python/
http://es.wikipedia.org/wiki/N%C3%BAmero_primo
http://es.wikipedia.org/wiki/N%C3%BAmeros_primos_entre_s%C3%AD
http://www.slideshare.net/jpadillaa/criptografia-asimetrica-rsa

martes, 11 de septiembre de 2012

Reporte # 1

Automatización y Control de Sistemas Dinámicos

Para esta ocasión hay que realizar la Función de Tranferencia de la idea del proyecto que tenemos contemplado para esta materia.

Primeramente en que consiste nuestro proyecto:

"Sera para el control del cautín, en especifico controlar la cantidad de temperatura que ha producido el cautín, para así regular la temperatura y evitar que ocurran incrementos que puedan dañar algún componente."

Entendido lo anterior, lo siguiente seria la función de transferencia:

Función de Transferencia: Función que nos permite relacionar la salida de un proceso, proyecto con la entrada de este.

La entradas y salidas serian acciones que produciría este proceso, comúnmente tienden a ser funciones o ecuaciones.

Para nuestro problema la entradas seria el cantidad de voltaje que entra al cautín para que este funcione, la temperatura, la masa de este y el material de la punta del cautín; la salida sería el calor y la temperatura del cautín.

De los valores anteriores solo del calor y de la intensidad de voltaje necesitaremos sus formulas.

Calor

$Calor (Q) = cm\Delta T$

Q = Calor producido
c = Calor especifico del material la punta
m = masa del cautín.
$\Delta T$ = Diferencia de Temperatura (Temperatura Final del cautín - Temperatura inicial del cautín)

Voltaje

$I = \frac{V}{R}$